Mengenlehre

Einleitung

Stell dir vor, du planst eine Party und erstellst eine Gästeliste. Diese Liste der eingeladenen Freunde ist eine Menge, die in der Mathematik beispielsweise so aussehen könnte:

$M = \{ \text{Anna}, \text{Ben}, \text{Clara}, \text{Mila}, \text{Yasmin}, \text{Zaid} \}$

Hierbei stellt $M$ die Menge der eingeladenen Freunde dar, und die Elemente der Menge sind die Namen der Gäste.

Mengenoperationen

Zeichen	$\LaTeX$	Name	Bedeutung
$\cup$	\cup	Vereinigungsmenge	Menge aus $A \land B$
$\cap$	\cap	Schnittmenge	Überschneidung von $A \land B$
$\setminus$	\setminus	Differenzmenge	Menge aus $A-B$
$\times$	\times	Kartesisches Produkt (Kreuzprodukt)	Menge aus $A = \{a,b,c\}$ und $B = \{1,2\}$*

*) $A \times B =\{(a,1),(a,2),(b,1),(b,2),(c,1),(c,2)\}$

Dein Partner hat nun auch eine Liste seiner Freunde erstellt:

$N = \{ \text{Anna}, \text{Nikolai}, \text{Oksana}, \text{Yasmin}, \text{Zaid}, \text{Zara} \}$

Folgende Möglichkeiten können sich daraus ergeben:

1. Alle Freunde einladen: $M \cup N = \{ \text{Anna}, \text{Ben}, \text{Clara},\text{Mila}, \text{Nikolai}, \text{Oksana}, \text{Yasmin}, \text{Zaid}, \text{Zara} \}$
2. Gemeinsame Freunde einladen: $M \cap N = \{ \text{Anna}, \text{Yasmin}, \text{Zaid} \}$
3. Nur Freunde von $M$ einladen: $M \setminus N = \{ \text{Ben}, \text{Clara}, \text{Mila} \}$
4. Nur Freunde von $N$ einladen: $N \setminus M = \{ \text{Nikolai}, \text{Oksana}, \text{Zara} \}$

Hieraus ergibt sich:

$ M \cup N \iff (M \setminus N) \cup (M \cap N) \cup (N \setminus M) $

Mengenrelationen

Zeichen	$\LaTeX$	Name	Beispiel
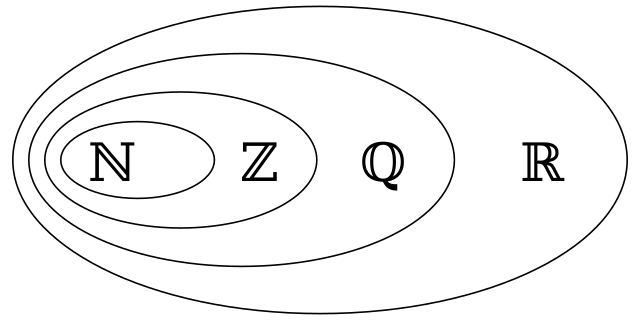
$\subset$	\subset	Teilmenge	$\mathbb N \subset \mathbb R$
$\supset$	\supset	Obermenge	$\mathbb R \supset \mathbb N$
$\in$	\in	Element von	$1 \in \mathbb N$
$\notin$	\notin	kein Element von	$-1 \notin \mathbb N$

Hier lassen sich wunderbar die Erkenntnisse der Logik anwenden:

$\mathbb I \not\subset \mathbb Q \iff \overline{\mathbb I \subset \mathbb Q}$

Zahlenmengen

Zeichen	Bedeutung	Beispiele	Definition
$\mathbb P$	Primzahlen	$2,3,5,7,11,13$
$\mathbb N$	Natürliche Zahlen	$1,2,3,4,5$	$\mathbb Z^+ \setminus 0$
$\mathbb Z$	Ganze Zahlen	$-3,-1,0,1,2,3$
$\mathbb Q$	Rationale Zahlen	$\frac{3}{4},\frac{1}{2}$
$\mathbb I$	Irrationale Zahlen	$0,33\overline 3$	$\mathbb R \setminus \mathbb Q$
$\mathbb R$	Reelle Zahlen	$0,4563$ oder $33\overline 3$ oder $\frac{3}{4}$
$\mathbb C$	Komplexe Zahlen	$z = 2+3\mathrm i $	$\mathrm i^2 = -1 $

TIPP: Zahlenmengen lassen sich in $\LaTeX$ mit \mathbb R ($\mathbb R$) darstellen. Konstanten mit \mathrm i ($\mathrm i$).

Distributivgesetze