Komplexe Zahlen

Einleitung

Nach dem Fundamentalsatz der Algebra hat jede algebraische Gleichung der Form:

$$ a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0 = 0 $$

genau $n$ Lösungen.

Beispiel

$$ \begin{aligned} x^2+1 &= 0 \\ x^2 &= -1 \\ x_{1,2} &=\pm\sqrt{-1} \\ x_{1,2} &=\pm\sqrt{i^2} \\ x_1 &= -\mathrm i \\ x_2 &= \mathrm i \\ \end{aligned} $$

Bezeichnungen

• $x$ heißt Realteil von $z$, $\Re z=x\in\mathbb{R}$
• $y$ heißt Imaginärteil von $z$, $\Im z=y\in\mathbb{R}$
• Eine Zahl der Form $\mathrm iy$ heißt imaginär
• $\mathrm i$ heißt imaginäre Einheit

Achtung: Der Imaginärteil ist nicht imaginär, er ist reell.

$$ \begin{aligned} z = 3+2\mathrm i => \Re z &=3 \\ \Im z&=2 \textbf{, nicht } 2\mathrm i \\ \end{aligned} $$

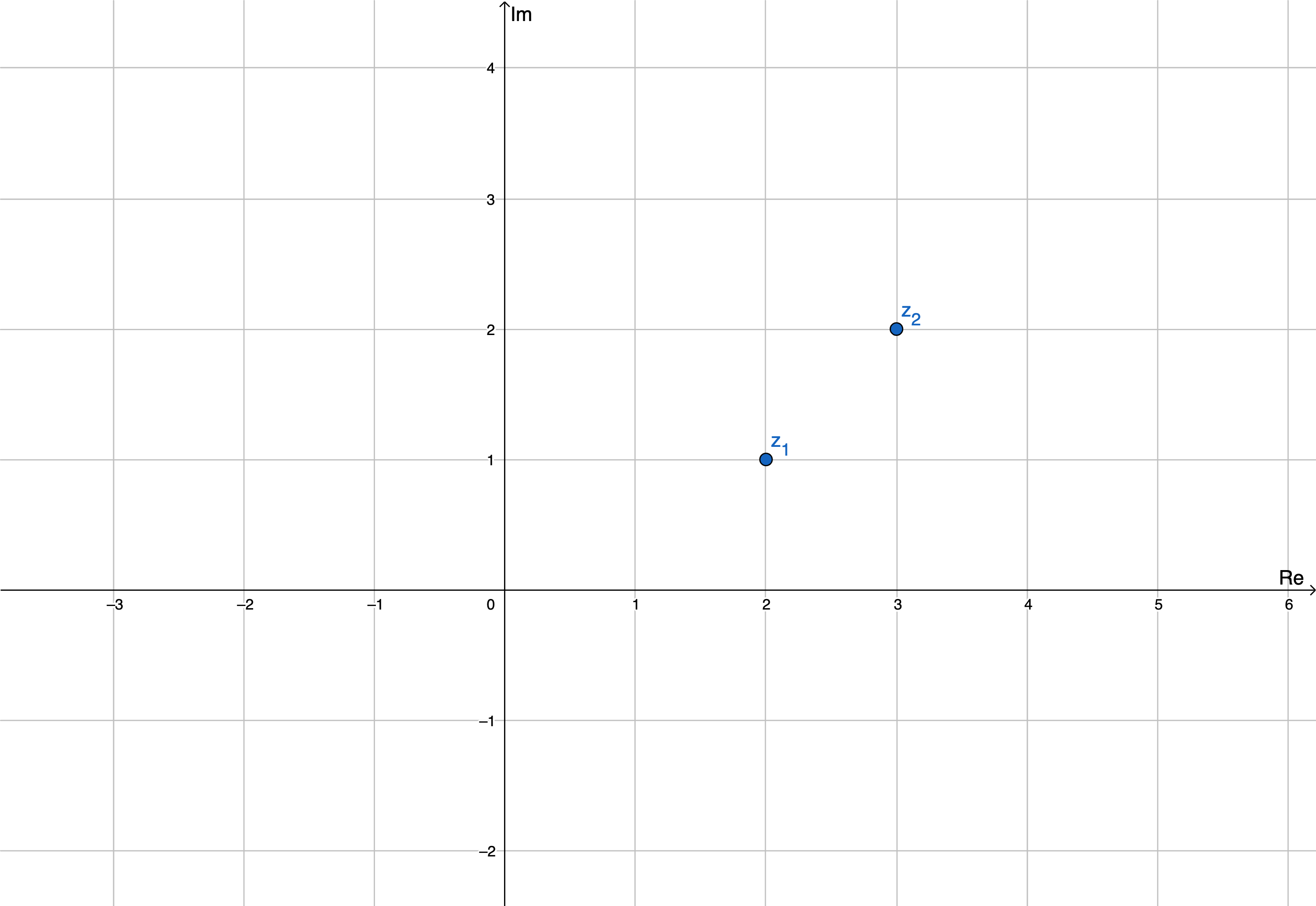
Komplexe Zahlenebene

1. $z_1=2+\mathrm i$
2. $z_2=3+2\mathrm i$

Rechenregeln

Summe

\begin{aligned} z_1+z_2 &= (x_1+\mathrm iy_1)+(x_2+\mathrm iy_2) && \\ &=x_1+x_2+\mathrm i(y_1+y_2) && \\ \end{aligned}

Produkt

\begin{aligned} z_1z_2 &= (x_1+\mathrm iy_1)(x_2+\mathrm iy_2) && \\ &= x_1x_2-y_1y_2+\mathrm i(x_1y_2+x_2y_1) && \\ \end{aligned}

Geometrische Bedeutung

Um die geometrische Bedeutung zu erkennen, müssen wir den Abstand $r=\sqrt{x^2+y^2}$ Pythagoras) und den Winkel $\phi$ ($x=r\cos\phi$, $y=r\sin\phi$) einführen.

Übertragung auf den Realteil

\begin{aligned} z_1z_2 &= x_1x_2-y_1y_2+\mathrm i(x_1y_2+x_2y_1) && \\ \Re (z_1z_2) &= x_1x_2-y_1y_2 && \\ &= r_1\cos{\phi_1}r_2\cos{\phi_2} - r_1\sin{\phi_1}r_2\sin{\phi_2} && \\ &= r_1r_2\cos(\phi_1+\phi_2) = \Re z_3 && \\ \end{aligned}

Übertragung auf den Imaginärteil

\begin{aligned} z_1z_2 &= x_1x_2-y_1y_2+\mathrm i(x_1y_2+x_2y_1) && \\ \Im (z_1z_2) &= y_1x_2+x_1y_2 && \\ &=r_1\cos{\phi_1}r_2\cos{\phi_2}+r_2\sin{\phi_2}r_1\sin{\phi_1} && \\ &=r_1r_2\sin(\phi_1+\phi_2) && \\ &=r_1r_2\sin(\phi_1+\phi_2) = \Im z_3 && \\ \end{aligned}

Geometrische Darstellung

\begin{aligned} r_3 &= r_1r_2 && \\ \phi_3 &= \phi_1+\phi_2 && \\ \end{aligned}