Digitaltechnik
Operatoren
| Mathematisch | Technisch | Name | Bedeutung |
|---|---|---|---|
| $\land$ |  |
Konjunktion | Und-Verknüpfung |
| $\lor$ |  |
Disjunktion | Oder-Verknüpfung (inklusiv) |
| $\veebar$ bzw. $\dot\lor$ bzw. $\oplus$ | 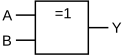 |
Disjunktion | Oder-Verknüpfung (exklusiv) |
| $\overline\land$ |  |
Konjunktion | Nicht-Und-Verknüpfung |
Wahrheitstabelle
| $A$ | $B$ | $A \land B$ | $A \lor B$ | $A \oplus B$ | $A \overline\land B$ |
|---|---|---|---|---|---|
| $W$ | $W$ | $W$ | $W$ | $F$ | $F$ |
| $W$ | $F$ | $F$ | $W$ | $W$ | $F$ |
| $F$ | $W$ | $F$ | $W$ | $W$ | $F$ |
| $F$ | $F$ | $F$ | $F$ | $F$ | $W$ |
Funktionen
\begin{flalign} Y &= (\overline{X1} \land X2) \lor (X1 \land \overline{X2} ) & \\ \end{flalign}
Algebra
- $\cdot$ entspricht $\land$ ($a \cdot b = a \land b$)
- $+$ entspricht $\lor$ ($a + b = a \lor b$)
Vollständige Systeme
Karnaugh-Veitch-Diagramme
Disjunktive Normalform
Kanonische DNF
In allen Termen sind alle Variablen negiert oder nicht negiert vorhanden.
Primtermdarstellung
Motivation
- Darstellung möglichst kurzer boolescher Ausdrücke
- technische Realisierung logischer Funktionen
Vorbemerkung
Implikation
Für jede Belegung, für die $g$ den Wert $1$ hat, nimmt auch $f$ in ihrem Definitionsbereich $D$ deb Wert $1$ an.
$$g \to f = 1$$
Nur Konjunktionsterme sind Kandidaten für Implikanten. Das schließt Disjunktionsterme (Oder-Termine) aus.
Minterme, die sich nicht weiter zusammenfassen lassen, sind auch Primterme.


